

「共振」という言葉の意味とは
「共振」と一言で言っても、それが電気の話だったり機械の話だったりして、会話が噛み合わなかったことはないでしょうか? 当社の場合、Z-Moveという機械的な耐振動性に優れたコネクタをリリースしていることもあり、8~9割の人間は共振と言えば機械的共振を思い浮かべます。電気の共振の話をする場合には、しっかり念押しをしておかないと混乱してしまう人が出てきます。その時関わっている仕事や専門分野で同じ言葉から違うものを思い浮かべてしまうのですね。あるいは共鳴という言葉もあって、共振とは何が違うのか?どう使い分けたら良いのか?等、共振ってよく耳にする言葉ですが意外とややこしいです。
例えば「破壊」という言葉は物理的にものをぶち壊すだけではなく「価格破壊」「体制を破壊する」「常識を破壊する」等と現象や状態に対しても使われますが、さほどややこしいと感じる人はいないでしょう。ちなみに破壊とは「何らかの力や影響が加わることにより、そのものの形状・機能・性質などが失われること。また、それを引き起こす行為のこと」だそうです。
「共振」も、この「破壊」といったような言葉のレベルまで落とし込めれば、きっと違う状況でその言葉が提示されても混乱せず直ぐに腑に落とせると思います。今回は共振の意味を整理しながら、個別の技術的な部分に触れて行ければと思います。
Resonanceを訳す:共振か共鳴か?
共振と共鳴は実は同じ英語「Resonance」を訳した結果なのです。つまり、少なくとも英語では区別されないのです。この言葉を訳すときに物理学の世界では「共鳴」が好まれて使われました。音を伴う現象から使われ出したものがそれ以外の振動に関しても、この訳を当てるのが一般的になったようです。
一方で工学の分野では「共振」という訳を当てられることが多かったようで、これは電気回路の共振現象などで「共鳴」=「共に鳴る」とするのに違和感があったからかもしれませんね。(共鳴も使われることがありますが)要はどちらも同じ現象=Resonanceを指していて、本質的な違いはなくちょっとした属するソサエティの違いで好みの呼び方が違っているだけなのですね。関東でごみを捨てるというのを、関西では放る(ほる)、北海道では投げるというようなものでしょうか? どちらを使っても間違いではないので、使う言葉が違っても混乱せずお互いを尊重し仲良くしましょう。
共に振るえる、共に鳴るとはどういう状態か?
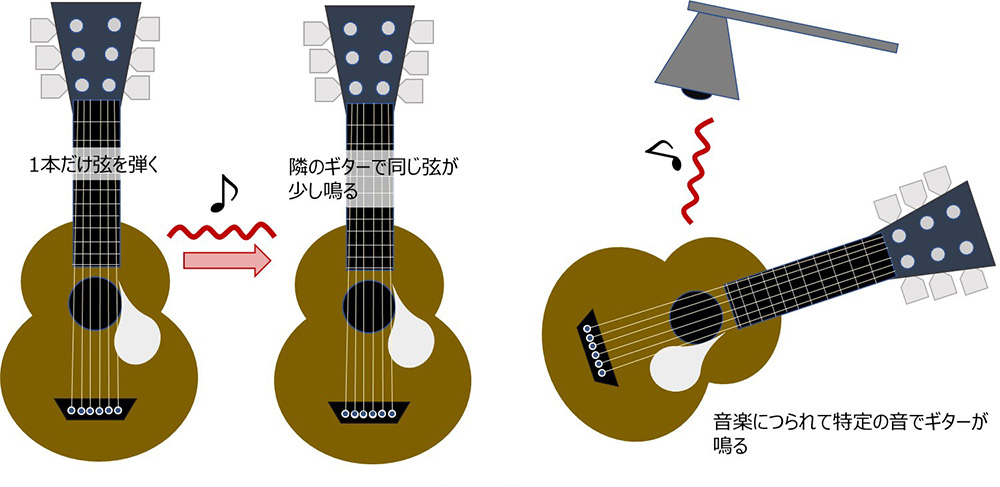
身近な現象ということで、共鳴の話から。ギターが2台ある状態で、一方のギターの弦を弾くと隣に置いてある触ってない方のギターの同じ弦が鳴ったりします。また、もっとレアなケースでかなり大きな音で音楽を聴いてないと起こりませんが、音楽につられて特定の音で「ポ~ン♪」と勝手にギターが鳴ることもあります。これが共鳴、すなわち共振です。
身近な共鳴現象
共振のイメージ
すなわち共振とは、近くである動きをしているものがある時に、ほんの少しの影響のはずなのにつられて同じ動きをしてしまう現象です。どんな場合でもつられてしまうのかというとそうではなくて、ある特定の、後述する固有周波数というものですが、「影響を受けやすい周波数の動き」の時だけつられて動き、かつ元は小さな影響力でもそれが続くと、どんどん大きくなってしまう現象を共振/共鳴と呼びます。これは電気回路でも物理的なものでも同じですが、前述のギターの例でいうと、弦の出す音程の周波数にあたります。また、近くにいる相手がランダムな周波数の動きを持っている場合には、その影響を受けやすい周波数の振動のみを抜き取った形でトレースして動きます。音楽に対して、特定の音に反応したギターの弦が鳴るようなものですね。イメージとしては次の図のようになるでしょうか。
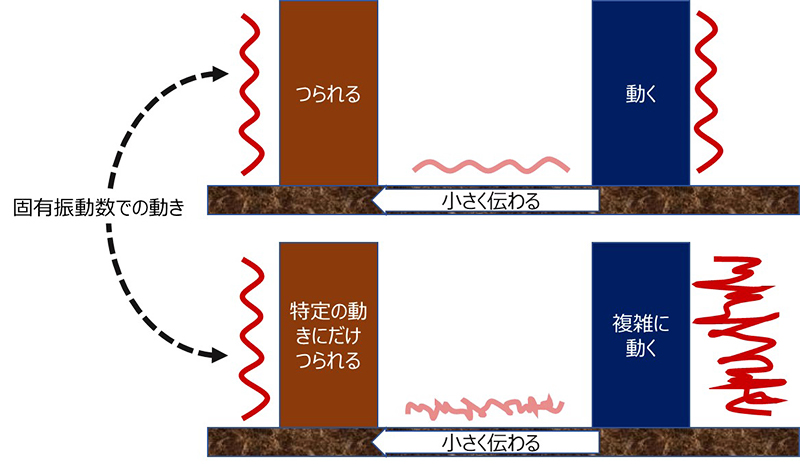
ではこういった現象の起こる、敏感になる周波数=固有振動数について、機械的なものと電気的なものの違いを説明していきたいと思います。
固有振動数 機械的な振動は質量、剛性、振動の重心点等で決まります
剛性と質量=音の高さで感じる影響
すべてのもの、あるいは部位といった方良いかもしれませんが、それが振動しやすい固有の周波数を持ちます。大雑把に言えば、その振動区間の質量と剛性で決まります。
剛性が高い方が、周波数は高くなります。ピンと張りつめた弦は緩く張られた弦より高い音がしますし、固いもの=ガラスの方がプラスチックより叩けばチーンとずっと高い音が鳴りますね。プラスチック同士でも、体感で固いものの方が高い音でなるイメージを持っている人は多いと思います。
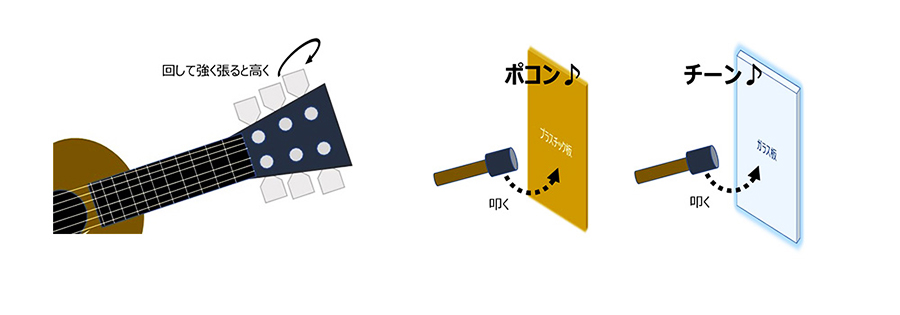
質量は小さい方が高い周波数になります。
同じ材質で質量、すなわち大きさと異なる場合では、小さいグラスは大きなグラスより高い音がしますし、木琴や鉄筋のプレート長さと音程の違いもそうです。細い弦は太い弦より高い音がします。
(大きさ/形状が同じで質量が異なる例というのは、身の回りでは質量の高いものの方が剛性も高いことが多いので、固有振動数=音の高さもトレードオフで難しいですが・・・・。)
ガラスと金属の板を叩いた時の音の違いという当たりのイメージが近いでしょうか。
音の話が多くなったところで、よく歌声でガラス、例えばワイングラスを割るような描写がフィクションの世界では見られます。
あれもワイングラスの固有振動数にあった音をぶつけているということで、まさに共振現象ですね。実際には人間の声レベルでワイングラスを割ることはかなり難しいようですが、スピーカから出した音でワイングラスを割るような理科の実験は色々やられているようです。
WEB上にも色々な実験結果レポートや動画が上がっていますので、興味のある方は検索をしてみてください。
すぐに複雑になる固有周波数
グラスをつるした時とテーブルに置いた時、あるいは手に持った時では音の高さが違ったりしませんか? これは周辺の影響で振動範囲の質量や剛性が変わっているためです。もう少し単純な事例ではギターの弦を抑えれば音程が変わり高くなる、これは振動の支点が変わったことで支点間の質量が小さくなったことによります。固有振動数の決定には様々な要因が関わっていそうです。
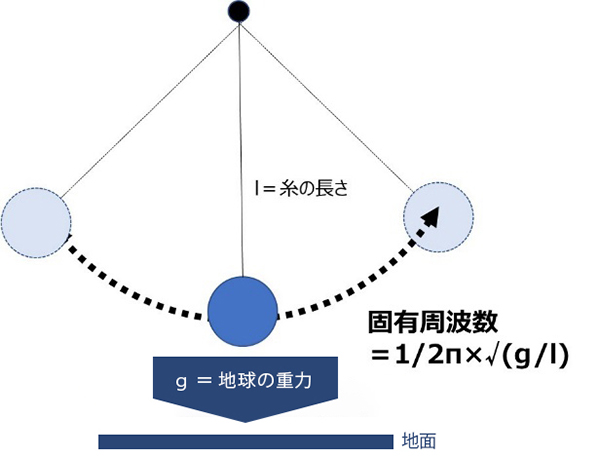
高校の物理で習うようなバネ、振り子あるいは楽器の弦等では、比較的シンプルな計算で固有振動数が求められます。特に振り子の振動数は「糸に質量がなく、重りに大きさがない(あるいは重心が糸の先端になるような)理想的なものであれば、質量やものの剛性にも関係なく、地球の重力=gと糸の長さだけで振動する周波数が決まり、1/2π×√(g/l)となります。振り子の糸の長さが長ければ周波数は低く、短ければ高くなります。ギターの弦と同じですね。
ここで、振り子からパッと連想するのはブランコでしょうか? しかしブランコではこのように単純にはならないのです。振り子にあたる糸は鎖なので質量は無視できませんし、背の高低で重心が変わったり、手で鎖を持つと支点も変わったり、ましてや乗っている人が上下に運動することでかなり複雑な現象になってしまいます。もう簡単に計算式化出来ませんね。ちなみに他の条件が同じで背が高い低いだけであれば、定性的には背が高い方が固有周波数は高く、また座り漕ぎより立ち漕ぎの方がやはり高くなります。振り子の式と見比べてみてください。
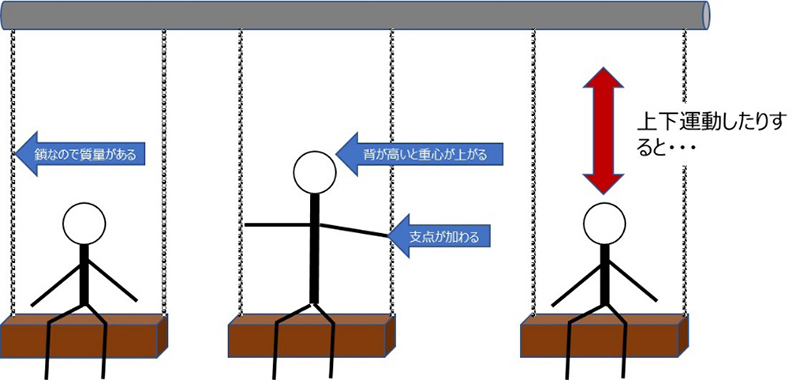
振り子からブランコでもちょっとした要素が加わったことで固有振動数の計算が難しくなりました。世にあるものは形状も複雑で、振動の支点となる部分が多数あったり色々なものが組み合わさっていたり、振動部位の重心点もまちまちですのでかなり複雑な計算が必要になります。例えば部品が実装された基板では、ねじ止めされている部分が振動の支点になったり、支点間に実装された部品各々の質量が振動の重心に影響を与えたりしますので、一筋縄では振動の状態を把握できません。部位ごとに複数の固有振動数が存在していたりもしますし、位相も異なったりもします。
一方で、「共に振るえる、共に鳴るとはどういう状態か?」で説明したように「元は小さな影響力でもそれが続くと、どんどん大きくなってしまう現象」が共振/共鳴であり、それは固有振動数で起こります。ものが使われる、おかれる環境には様々な外部要因があって、本当にその環境下で安心・安全に使えるのかを判断するには、固有振動数や使用環境下で共振の発生する可能性などを把握しておく必要がありますね。
CAEによる振動解析とイリソが提供する「振動解析サービス」
このような複雑な振動の現象を解析するために有限要素法等を用いたCAEによって、振動解析を行い実際のものがどのような時に共振現象を起こし、その共振に耐えられるのかを解析することがあります。一つ一つ手計算で検証するのは困難でも、例えば部品が実装された基板を構成する部材毎の質量や剛性等を元にその製品を解析することで、様々な問題を事前に予期できます。コネクタの選定においても、それは重要です。
イリソ電子工業では、当社製品の仕様を検討されるお客様へ振動解析サービスを実施しており、最適な製品の提案や解析結果によっては基板レイアウトの変更まで踏み込んだご提案も行っています。リンク先でそちらのサービスのご紹介もしています。コネクタにとって振動がどのような問題をもたらすのか等も少し説明していますので、是非ご覧ください。
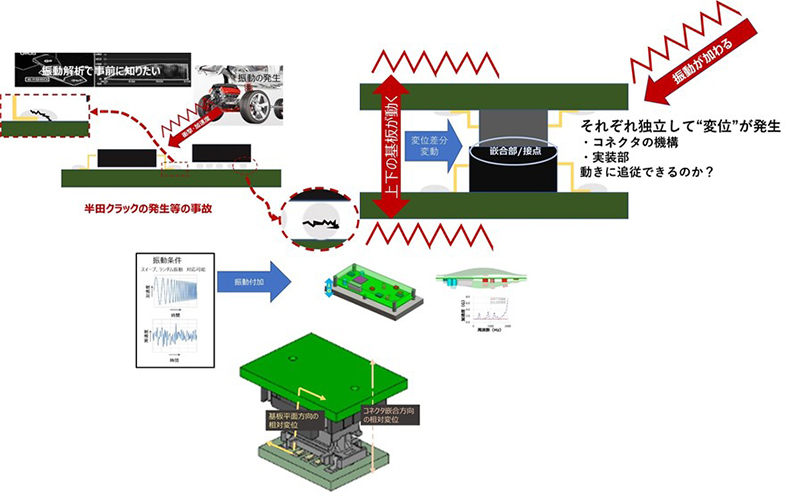
では次は電気の共振現象にお話を移してみようかと思います。
電気の共振はややこしい?
「電気は見えないからわからない!」
電気工学系ではない方がそうおっしゃっているのを耳にします。機械的な共振のベースである振動は見て判ったり、聞いて音程で違いを感じられたり、触ったり、その場に居て感じたりとまだわかりやすいのですが、電気で共振と言われてもイメージしにくいかもしれません。私は学生時代電気工学を学んでいましたが、それでも時々迷子になることがあります(真面目に学んでなかったからという可能性には、ここでは目をつむります)。生産現場の管理などに有効な手法として「見える化」というものがあります。例えば、生産の進捗具合や不良の発生状況等々、一目ではわからないものを皆の目に見える形にして共有しようというものです。他の電気にまつわるコラムでも気に留めている点ではあるのですが、可能な限り見て判るような工夫をして説明したいと思います。
交流と周波数と位相
中学校の理科で習うかと思いますが、電気には直流と交流というものがあります。(信号に使われる電気は直流成分や交流成分と言われるように複合体だったりしますが、一旦置いておきます)
交流のメリットとしては変圧しやすいから等(関連する有名なところでは、エジソンに勝った弟子のニコラ・テスラさんという人が居るので興味のある方は調べてみてください)ですが、これからの話につながっていくので信号伝送にも交流的な挙動の把握が重要という点だけは頭の隅に置いておいてください。
さて、日本の関東で暮らす方々の家庭に送られてくる電気は一般的に「交流・50Hz・100V電圧」になります。
関西は60Hzですが、キリが良いので説明しやすい50Hzの方で進めさせてください。
50Hz=1秒間に50周期という単位なのですが、例として0.15秒間での50Hzの電気の動きを図示してみました。
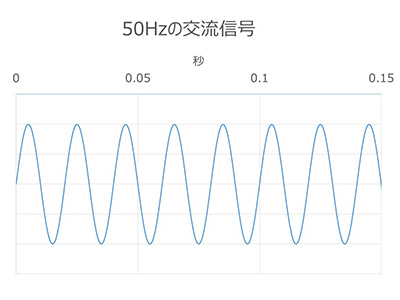
0.15秒間にこれだけ動くと、目には見えませんがまさにブルブルと振動しているような状態です。
そして、周波数の違う電気もあります。
周波数が100Hz=倍になると、より忙しくブルブル震えます。音でいうと高くなった感じです。ちなみに倍ですからオクターブの違いですね。少し話はそれますが、倍なのになぜオクターブ=オクタ=8なのかというとドレミファソラシドの8個目が1個目と同じドだからですが、そもそも7音階になった理由は気持ちの良い響きと音階の整合を取ろうとして自然とそうなったのだとか。オクターブや良い響きという所に共振/共鳴を示唆する部分がありますね。
図では2倍にとどめましたがこのブルブルの回数はもちろん10倍、100倍、1000倍・・・・メガは100万倍、ギガは10億倍と、際限なく早いものがあり、高周波と呼ばれる領域になっていきます。
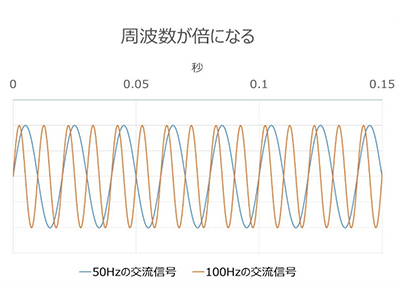
一方で位相という考え方があります。
同じ周期のブルブル、同じ周波数の電気でも、始まりと終わりのタイミングはさまざまで、比較した時の違いを位相のズレと言います。
共振の話へ移行するときにこの3つの図のイメージが重要になりますので、何となくでも理解をしていただけると嬉しいです。
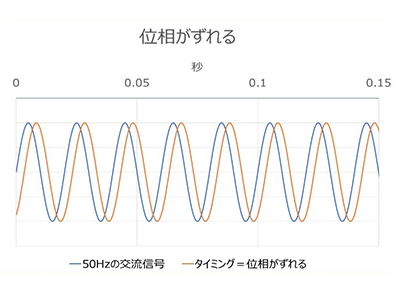
振動も交流も波で干渉する
まず干渉とは何でしょうか。干渉とは、「二つ以上の同一種の波動が同一点で合ったとき、重なって互いに強めあい、または弱めあう現象」です。揺れる回数のことを周”波”数と呼ぶように、前項で説明したような交流の電気も、ものを揺らす振動も波です。したがって、二つ以上のものが重なると強め合ったり、打ち消しあったりするのです。
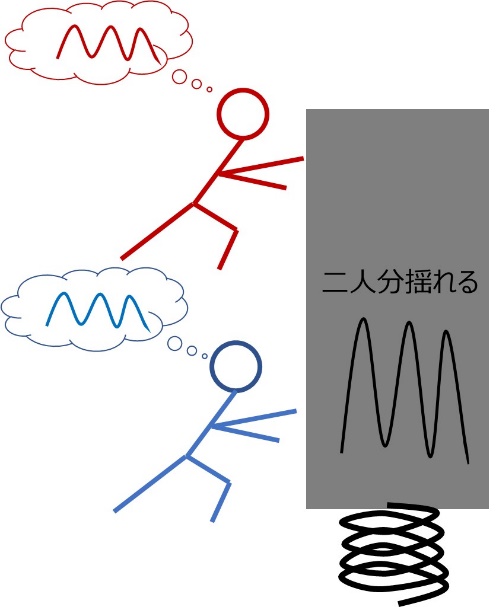
丈夫なバネの上に乗っかった、大きくて重いものを同じ力を持った二人が協力して上下に揺らそうとしている所を想像してください。
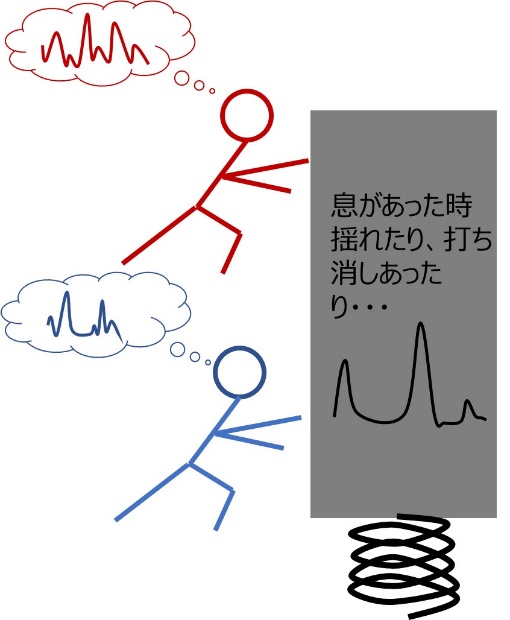
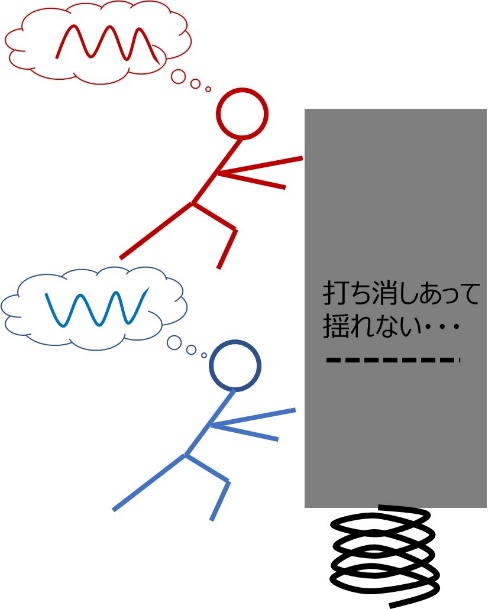
二人の息がぴったり合っていれば、力が合わさって大きく揺れるでしょう。二人が適当にゆすっていると、たまたま息があった時だけ大きく動いて、後は小さくしか動かなかったり逆方向の力同士打ち消しあって動かなかったりです。二人が全く逆の動きをさせようとすれば、完全に打ち消しあってうんともすんとも言わなくなりますね。電気でも似たようなことが起こるのです。ここまでが、前提として抑えてもらいたいイメージでした。
では、電気で共振と呼ばれる二つの現象の説明に話を移します。
電気の共振
① インピーダンスの消失と無限大
「インピーダンスって何ですか?」と問われれば「電圧÷電流です」と答えます。当社でインピーダンスというと「(特性)インピーダンスって何ですか?」という質問だったりするのですが、なるべく物事を正しく伝えようとするとそうなるのですね。インピーダンスマッチングやインピーダンスプロファイル等、誤解を招かない局面では特性/Characteristicという単語が省略されるので、業界によってはインピーダンス=特性インピーダンスと捉えてしまっている人も多いのですが、あくまでもインピーダンスの中の特定のものなのです。尚、リンク先の用語集にも記載していますが実際に特性インピーダンスも「電圧÷電流」です。
「あれ?『電圧÷電流』ってオームの法則の(電気)抵抗じゃないの?」と思われた方、概ね正解です。抵抗もインピーダンスの一つなのです。直流でも交流でも電気抵抗はありますが、電気に動きがある交流になるとキャパシタンス(静電容量)とインダクタンスという要素/素子が登場します(キャパシタンスは直流でも蓄電的に扱われますが)。ここで電圧と電流の位相のズレという概念が出てきます。インピーダンスが大きさだけではなく角度を持つ複素数になる・・・・というとちょっとややこしいですが、単純な足し算で積み上げられなくなると思っておいていただければここでは十分かと思います。まずは抵抗・キャパシタンス・インダクタンスとはどんなものかを簡単に見てみましょう。
まずオームの法則でおなじみの抵抗です。
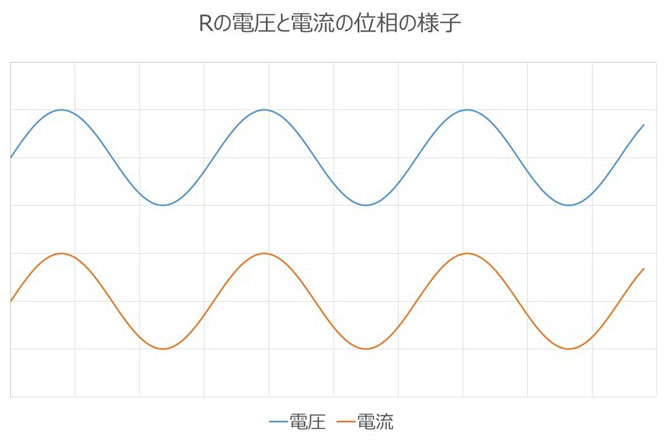
電気のエネルギーが熱に代わって失われます。電圧と電流の位相は同じで、インピーダンスは複素数的に言えば実数となります。単位はインピーダンスと同じくΩになります。コネクタや伝送線路での抵抗に関してはコラム内の「「抵抗損失」と「誘電損失」信号が熱に変わって小さくなる?」で、もう少し詳しく説明していますので、興味のある方はそちらも参照いただけますと嬉しいです。
抵抗:R
・電気を熱に変えて消耗(損失素子)
・周波数に依存しない
(現実世界では表皮効果などで上昇)
・素子内での電圧と電流の位相は同じ
次にキャパシタンスです。
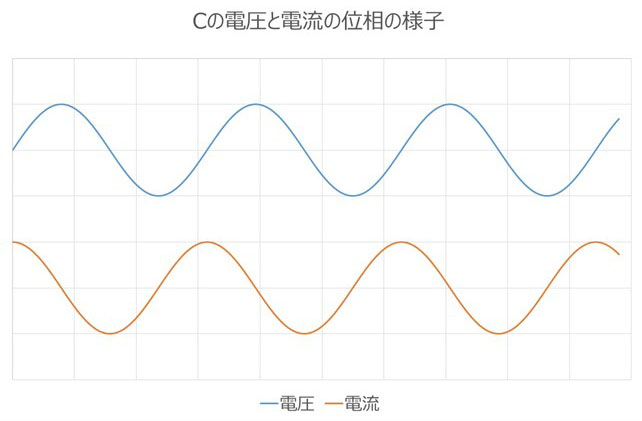
いわゆるコンデンサと言われるものは、このキャパシタンス機能を持った部品になります。電圧に応じた電気のエネルギーを蓄える、もしくはたまった電気の量で電圧が決まる素子で、その性質によってバランスが取れた後は直流の電流は通さず、電圧変化の急峻な周波数の高い電流程通しやすい特性を持つため、そちらを活かした使われ方もかなり多いです。位相は電流が電圧よりπ/2進みます。インピーダンスを複素数的に言えば、マイナスの虚数になります。インピーダンスの単位はΩですが、その前の素子の定数としてF (ファラド)という単位を持ちます。
キャパシタンス:C
・電圧に比例した電荷を蓄える(無損失素子)
・電圧が変わると余った・足りない電荷を
電流として取り入れたり吐き出したりする
・電圧変化の激しい高周波ほど電流が
流れやすい=インピーダンス低下
・電圧と電流の位相は図のようにずれる
最後に3つ目、インダクタンスです。
インダクタと呼ばれえる部品やコイルがこの機能を備えたものになります。電流の変化を嫌うため、電圧の変化に逆らった様な挙動を持ちますので、電圧が強制的に変わるような高周波ほど電流が流れにくくなります。位相は電流が電圧よりπ/2遅れます。インピーダンスを複素数的に言えば、プラスの虚数になります。インピーダンスの単位はΩですが、その前の素子の定数としてH (ヘンリー)という単位を持ちます。
インダクタンス:L

・電流の変化に逆らう電圧(無損失素子)
・電圧先なら動きがあるほど電流を抑えられる
・動きの激しい高周波ほど電流が
流れにくくなる=インピーダンス増加
・電圧と電流の位相は図のようにずれる
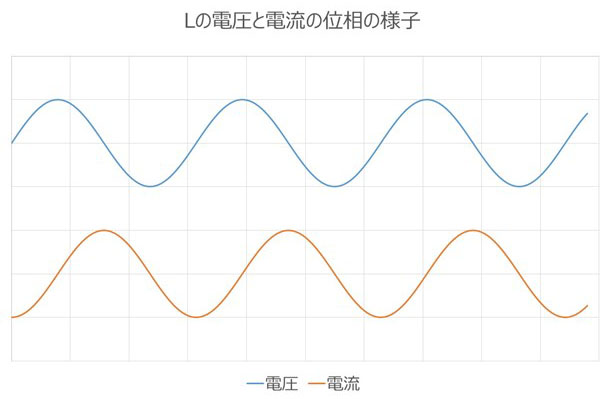
ここで、注目していただきたいのはCとLの電圧の電流の位相の関係が正反対だということです。
まずは、なんとなくLとCでは同じ電圧がかかっていれば「電流の波」が打ち消しあう、同じ電流が流れていれば「電圧の波」が打ち消しあうとイメージしてみてください。そもそも何故電圧と電流の位相が違うのかは、Cではたまったものを吐き出すたり足りない分を取り入れたりするとか、Lは変化を抑えようとするなどのワンクッションおいた対応がズレにつながるというイメージでも良いですし、もう少し数学的にCだとV=1/C×∫Idt(←たまった電気が電圧に比例するという式ですね)とか、LであればV==-L×dI/dt (←電流の変化に逆らった電圧が派生するという式ですね)といった簡単な微分積分の果てに説明も出来たりするので、興味のある方は調べたり、計算してみたりしてください。
また、お互いに負と正の符号を持つ虚数インピーダンスですので、単純な足し算は出来ないと言いましたがLとCだけで抵抗が居なければ、ややこしい複素数計算になりません(現実にはすべての部品に抵抗成分があるので、そう簡単にはいかないですが・・・・)。
一方で絶対値としてはCのインピーダンスは周波数の上昇に伴い小さくなり、Lの方のそれは大きくなっていきます。なんとなく特定の周波数で完全な打ち消しあいが発生しそうですね。
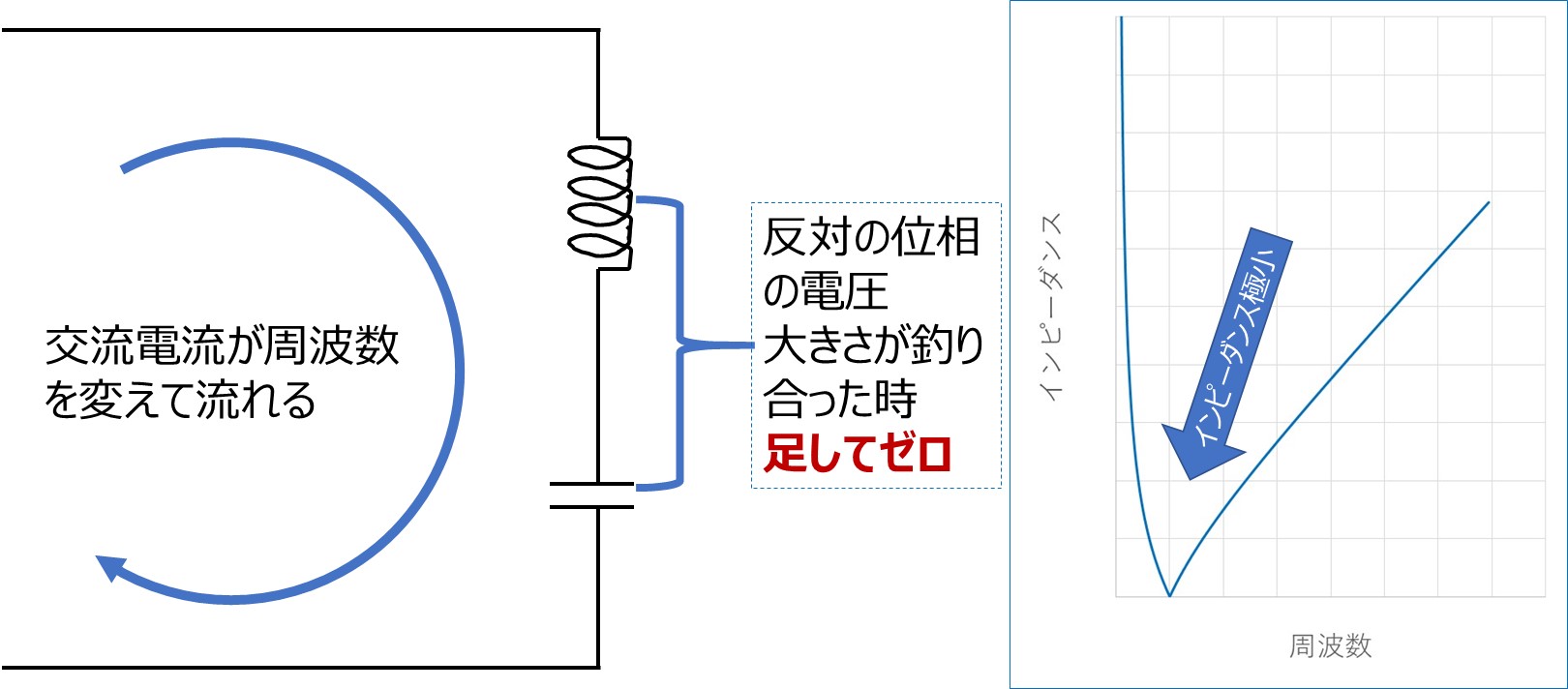
下の例では、CとLのインピーダンスのつり合いが取れるところピンポイントでお互いの発生している電圧の波が完全に打ち消しあいます。
電流が流れているのに電圧がゼロになりますからインピーダンスは0を何で割っても0になりますね。要は特定の周波数でショートが発生してしまうようなもので、ちょっとしたことでガツンと電流が流れる回路になります。
今度の回路では、CとLのインピーダンスのつり合いが取れるところピンポイントでお互いに流れている電流の波が完全に打ち消しあいます。素子部には電流が流れているのですが、自己完結していて外部からは電流が入ってこない状態です。
外から見たインピーダンスは電圧がかかっているのに、電流が流れないので極大=無限大となります。
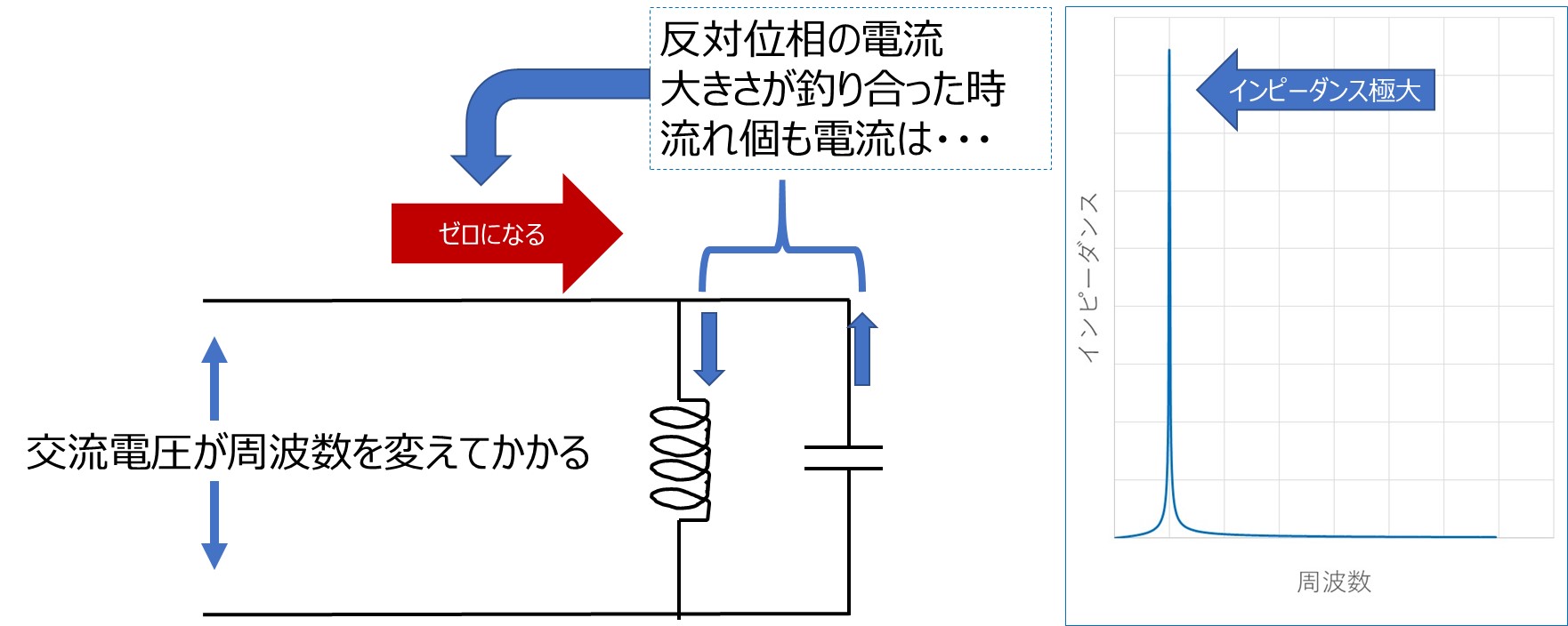
どちらの場合も極小もしくは極大は周波数f=1/(2π√(LC)) (Hz)で起こります。実際の部品や回路では様々な場所で抵抗成分を持つために、上に挙げた事例よりはややマイルドな特性を示しますが、それでもピンポイントでインピーダンスが極小化したり極大化したりします。電流がドカッと流れやすくなったり流れにくくなったりが特定の周波数ピンポイントで起こるこのような現象を電気の共振と呼びます(共振という言葉で表現されることがいまいち腑に落ちない人も居るかもしれませんが、実は自分もです)。こういった現象は特定の信号のみを通したり、妨げたりする回路にフィルタとして応用されます。
さて、ややこしいことに電気的な共振と呼ばれる現象はもう一種類あります。個人的にはこちらの方が共振の名を冠するのにふさわしい、イメージしやすい現象だと思っていますが、そちらに話を移していいます。
② 反射による共振
コラム内の「『フローティング』と『高速伝送』は相反する要求?」で特性インピーダンスと反射の影響について簡単に触れています。下の図はそのコラム内の「何故反射が問題なのか?」の項で使用した図の再掲になります。

この時は時間経過ととともに反射して重なる信号を「ノイズ」として問題としていました。
では、繰り返しの信号がそのまま乗ってくる場合はどうでしょうか。
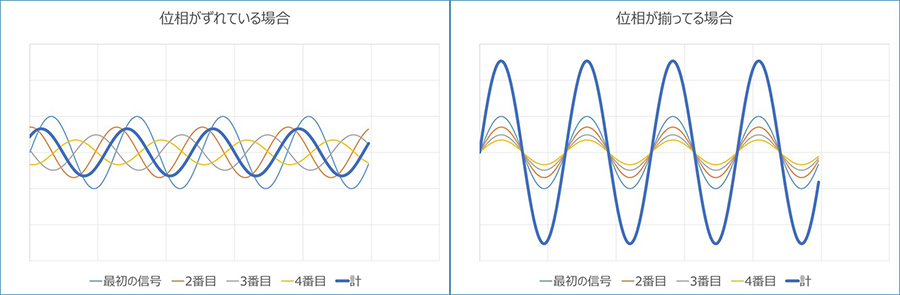
下記は簡略したものですが、少しずつ小さくなっていき位相もずれていく4つの波形を合計したものと、少しずつ小さくなっていきますが位相は「たまたま」ビシッとそろった場合のものを比較イメージとして並べてみました。左側では最初の波形とずれたものが小さくなって合波となっています。一方で、右側では最初の波形をそのまま大きくしたものが合波となります。
例えば最初に上げた「何故反射が問題なのか?」からの転用の図で言えば、ぐるっと回ってくる時間と、波の山と山の間の時間が揃っていればお互いに強め合いそうです(実際には反射には反転する負の反射というのもありますが、正の反射の場合と考えてください)。
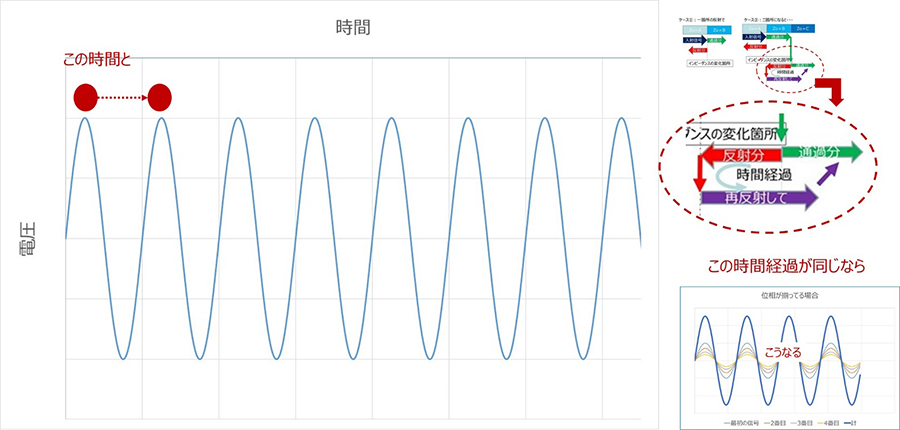
実際に有限長の信号線路で、両端で正反射が送る場合、波の周期と信号が端から端までを往復するのかかる時間が同じ場合、繰り返される反射による交流波(正弦波)の位相が揃うため、重ね合わせは干渉して強まります。線路の長さ=片道でいうと半周期分の時間がかかる長さとなりますので、波の長さの半分=1/2波長とも言えます。
実際に有限長の信号線路で、両端で正反射が送る場合、波の周期と信号が端から端までを往復するのかかる時間が同じ場合、繰り返される反射による交流波(正弦波)の位相が揃うため、重ね合わせは干渉して強まります。線路の長さ=片道でいうと半周期分の時間がかかる長さとなりますので、波の長さの半分=1/2波長とも言えます。

下記に一応波長の計算式は下記の通りです。
λ = (C/√ε) / f
λ = 波長 (m) C = 光の速度 = 3.08 × 108m /s εs = 線路周辺の(等価)比誘電率 f = 周波数 (Hz)
空気中(厳密には真空中)ですと、50Hzで約6000Km、1KHzで約300Km、100MHzで約3m、1GHzでようやく約30cmとなって、25GHzでは約12mmになります。1/2λ はそれぞれその半分ですね。空気以外の物質で周辺が満たされている場合は、これより短くなります。プラスチック系であれば、ものによって8割程度~1/3くらいです。
ところで反射が「片側だけ」負の場合は波が反転してしまうので、線路長が1/4λ に相当するような周波数が共振周波数となります。
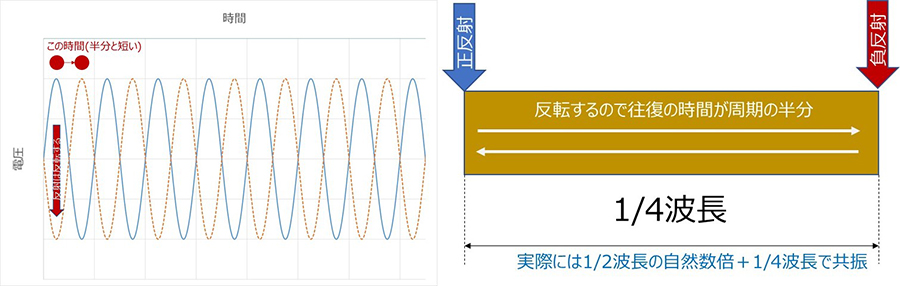
これはどちら側でも、片方のみならそうなります。両端とも負の反射の場合は、両端とも正の反射の場合と同じく1/2λ となる周波数が共振周波数となります。頭の体操として考えてみてください。ちなみに、線路の外側の特性インピーダンスが線路より低い場合は正反射(短絡で全反射)し、高い場合では負の反射が起こります(開放で全反射)。
反射による共振の弊害
さて、これが二つ目の電気の共振=反射による共振ですが、この現象は何をもたらすのでしょうか?
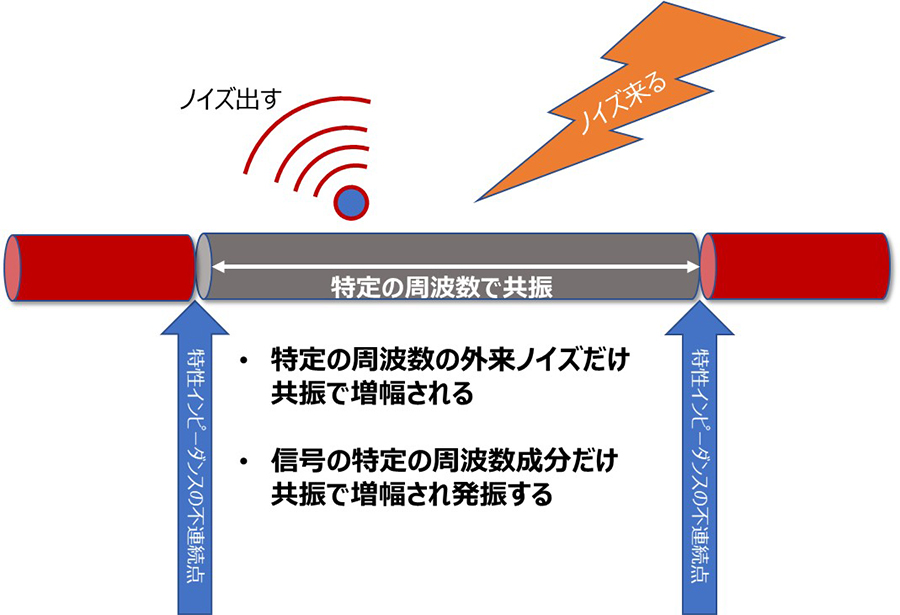
特定周波数のみ共振・増幅させるという現象はアンテナやフィルタなどにも有効活用出来ますが、ここではネガティブな部分を少し考えてみます。特性インピーダンスの不連続点に挟まれた線路を見てみましょう。この線路では両端で反射が起こりますので特定の周波数で共振が発生します。
信号が流れた時、特定の周波数成分だけ共振が起こるため、放出しやすくなります。また、外来ノイズも特定の周波数のものは元が小さくても、共振によって無視できないレベルになります。ところで、インピーダンスの不連続部で正の反射が起こるか負の反射が起こるかは意外と事前に把握するのは難しかったりします。ですので、線材や配線長等を設計するときには特に気になる周波数帯、例えば周囲に飛び交っていそうな無線信号帯や線路を流れる信号のメイン波数などですが、その長さとして1/2λ のN倍のものとそれ+1/4λ のものは可能であれば避けておいた方が良いです。
もう20年以上前の話になりますが、以前の仕事でお付き合いのあったエンジニアの方には、EMI系の対策のためいろんな要素を打ち込むと「公差込みで共振が起こらないケーブル長を決める」計算用エクセルスプレッドシートを自作し活用している方がいらっしゃいました(そのエクセルを「下さい!」と申し出たら「ノウハウなので・・・」と断られましたが)。 また、ある機器の接続用のケーブルを変えたら、突然EMI試験に落ち、シールド不良を疑っていたら実際は線材の誘電率の違いで丁度メインの周波数の共振長になっていたことが後に判明したという事例もうかがったことがあります。この2つの事例は、数m、㎝単位で発生していた問題でした。
一方で、コラム内の「『フローティング』と『高速伝送』は相反する要求?」に書かせていただいているように、電話通信時代に”km”単位で起こっていたことが、通信速度が上がり”Mbps”に入った時に”m”単位で起こるようになり、それが”Gbps”時代の現在は”mm”単位で発生しています。信号の高速化が進んできた現在で”mm”単位まで気にしていたら、すべてのものに対して共振長を避けていると何も使えなくなってしまいます。よって、線路間・部品間の接続や部品内部での特性インピーダンスの整合を取ることが非常に重要になっており、加えて、シールド対策や設置処理等も重要になってきます。(その辺りはサイト内「コネクタとは」の下部項目「コネクタの信頼性を向上させるオプション」でもほんの少し触れています)。
このように二番目の電気の共振現象によって、昨今我々コネクタメーカが取り組むべき課題もどんどん増えているのです。
まとめ
今回は複数の状況で用いられる共振/共鳴の言葉とシチュエーションによる混乱から始まり、機械的なものと電気的なものは2種類について説明させていただきました。
我々コネクタメーカにとっては、機械的なものも電気的なものも、対応・対策として取り組むべき課題を日々もたらすものです。デメリットのみではなく、有効な活用も考えられるテーマで良く知りよく考え、皆様のお役に立てる製品を次々と生み出して行ければ良いなと、日々研鑽を重ねております!

